低通滤波器理解

低通滤波器算是工程应用中比较简单的滤波方式了,当然这里针对的是一阶低通滤波器，低通滤波器的作用是可以过滤信号中的高频分量，使信号看起来更加的平滑，那这个过程是如何实现的呢，这里以一阶低通滤波器为例，详细解释低通滤波器的原理。

一阶低通滤波器可以由硬件电路实现，参与的元器件主要是电阻和电容，典型的一阶低通滤波器拓扑结构如下：

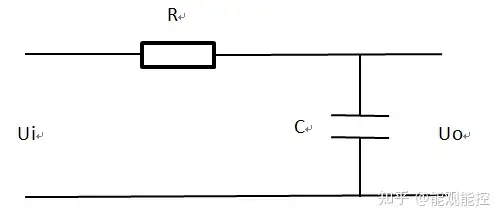
为分析其工作原理，将其表达成传递函数形式有：

U0(s)Ui(s)=1RCs+1(1)\frac{U_0(s)}{U_i(s)}=\frac{1}{RCs+1}~~~~(1)

这里强调一点，该低通滤波器的截止频率 wc=1RCw_c = \frac{1}{RC}

对其进行Z变换，即令 s=1−Z−1Ts=\frac{1-Z^{-1}}{T} ，其中T为采样采样周期，得到

Uo(z)Ui(z)=TRC(1−Z−1)+T(2)\frac{U_o(z)}{U_i(z)}=\frac{T}{RC(1-Z^{-1})+T}~~~~(2)

将其离散化，这里会用到几个公式，如下

U(z)=U(n)z−nU(z)=U(n)z^{-n}

U(n−1)U(n)=z−1\frac{U(n-1)}{U(n)}=z^{-1}

带入上式可以得到

Uo(n)=RCRC+TUo(n−1)+TRC+TUi(n)(3)U_o(n)=\frac{RC}{RC+T}U_o(n-1)+\frac{T}{RC+T}U_i(n)~~~~(3)

令 a=TRC+Ta=\frac{T}{RC+T} ，上式可化为

Uo(n)=(1−a)Uo(n−1)+aUi(n)(4)U_o(n)=(1-a)U_o(n-1)+aU_i(n)~~~~(4)

其中， Uo(n−1)U_o(n-1) 为上一次的滤波值， Ui(n)U_i(n) 为本次采样值，a为滤波系数。

这里可以给出结论，同样的具有一定频率的信号输入(低通滤波器对直流量无效)，a越大，说明这个低通滤波器的截至频率越大，滤波效果降低；反之，滤波效果增强，但随之而来的是信号的失真程度增大，各有利弊，需要根据不同的应用需求确定该滤波系数的大小。

下面对该结论进行原理分析

实际举个例子吧，输入信号 1+sin(wt)1+sin(wt) ，让该信号通过一个低通滤波器，以理论推导的方式解释其响应，以分析低通滤波器的原理。

低通滤波器的传递函数 G(s)=wcs+wcG(s)=\frac{w_c}{s+w_c} ,那么经过低通滤波器的信号输出为

y=(1+sin(wt))wcs+wcy=(1+sin(wt))\frac{w_c}{s+w_c} ,移相可得

y,+wcy=wc+wcsin(wt)y^,+w_cy=w_c+w_csin(wt)

该式为一阶非齐次微分方程，通解形式为 y0=Ce−wcty_0=Ce^{-w_ct} ,特解形式为

y∗=e−wct∫[(wc+wcsin(wt))ewct]dty^*=e^{-w_ct}\int_{}^{}[(w_c+w_csin(wt) )e^{w_ct}]dt

=e−wct[∫wcewctdt+∫wcewctsin(wt)dt](5)=e^{-w_ct}[\int_{}^{}w_ce^{w_ct}dt+\int_{}^{}w_ce^{w_ct}sin(wt)dt]~~~(5)

令 A=∫ewctsin(wt)dtA=\int_{}^{}e^{w_ct}sin(wt)dt ，则式(1)可化简为

e−wct[∫wcewctdt+wcA](6)e^{-w_ct}[\int_{}^{}w_ce^{w_ct}dt+w_cA]~~~~(6)

同时继续式(1)的推导:

=e−wct[ewct+∫sin(wt)dewct]=e^{-w_ct}[e^{w_ct}+\int_{}^{}sin(wt)de^{w_ct}]

=e−wct[ewct+ewctsin(wt)−w∫ewctcos(wt)dt]=e^{-w_ct}[e^{w_ct}+e^{w_ct}sin(wt)-w\int_{}^{}e^{w_ct}cos(wt)dt]

=e−wct[ewct+ewctsin(wt)−wwc∫cos(wt)dewct]=e^{-w_ct}[e^{w_ct}+e^{w_ct}sin(wt)-\frac{w}{w_c}\int_{}^{}cos(wt)de^{w_ct}]

=e−wct[ewct+ewctsin(wt)−wwc(ewctcos(wt)+w∫ewctsin(wt)dt)]=e^{-w_ct}[e^{w_ct}+e^{w_ct}sin(wt)-\frac{w}{w_c}(e^{w_ct}cos(wt)+w\int_{}^{}e^{w_ct}sin(wt)dt)]

=e−wct[ewct+ewctsin(wt)−wwcewctcos(wt)−w2wcA](7)=e^{-w_ct}[e^{w_ct}+e^{w_ct}sin(wt)-\frac{w}{w_c}e^{w_ct}cos(wt)-\frac{w^2}{w_c}A]~~~~(7)

通过式(6)和式(7)可得 A=wcsin(wt)−wcos(wt)w2+wc2ewctA=\frac{w_csin(wt)-wcos(wt)}{w^2+w_c^2}e^{w_ct} ,代入式(6)可得

y∗=1+wcsin(wt)−wcos(wt)w2+wc2y^*=1+\frac{w_csin(wt)-wcos(wt)}{w^2+w_c^2}

=1+wcw2+wc2sin(wt−φ)=1+\frac{w_c}{\sqrt{w^2+w_c^2}}sin(wt-\varphi) ,其中 φ=arctan(wwc)\varphi=arctan(\frac{w}{w_c})

最终可以得到经过低通滤波器的信号输出 y=y0+y∗=1+wcw2+wc2sin(wt−φ)+Ce−wcty=y_0+y^*=1+\frac{w_c}{\sqrt{w^2+w_c^2}}sin(wt-\varphi)+Ce^{-w_ct}

可以看到，输出由三项组成，1为原先信号输入的直流量，经过低通滤波器不会发生变化，第二项为输出的正弦量，发生了幅值衰减和相位滞后，程度受截止频率和当前输入信号的影响，当输入信号不变时，截 止频率越大，信号失真程度越低；当截止频率不变时，输入信号的频率越高，信号幅值衰减越严重，相位滞后也越大，第三项为衰减项，截止频率越大，衰减速度越快，最终趋向于零。当输入频率等于截止频率时，此时信号衰减为为原来的0.707倍，相位滞后45度。

经过理论推导后，低通滤波器原理可以比较明确的理解了，根据式(4)可以很快的通过代码的形式实现低通滤波器的性能，同时也可以通过调整硬件电阻的阻值和电容的容值实现低通滤波器的功能。

，