正弦交流波形

开篇：世界上各发电厂普遍发出的多为正弦电压，其应用遍布电气、电子、通信、工业系统等。此外，因为正弦交流电本身的许多特殊性质，若将其施加在基本电气元件上将产生某些独特的结果。直流电路中的大部分定理、定律也能够应用在正弦交流电路中。

A.C：Alternating Current

交流电压：电压大小以某种方式交变，如图1所示：

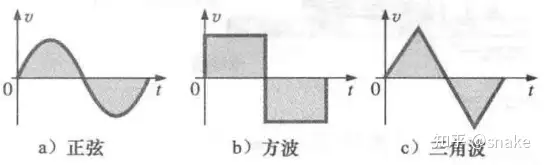
图1 a)为正弦交流电压。

正弦交流电压的获得：大多数电厂主要依靠水力、燃油、天然气、核能等能源来发电，无论哪种发电方式，交流发电机都是能量转换过程中的关键部分。上述能源产生的能量通过转轴驱动转子转动，转子含有磁极，并且位于定子（静止的）内容，在定子绕组中产生感应电压，由法拉第电磁感应定律可知感应电压为：

e=NdΦdte = N\frac{d\Phi}{dt}

通过调整发电机参数，就能够获得正弦交流电压。

为了保护自然资源、减少污染，风能、太阳能和燃料电池等在世界各地得到了广泛关注。风力发电机，其旋转叶片直接与交流发电机的轴相连，对外提供交流电压；太阳能电池，是通过吸收光子的能量产生直流电压，再通过逆变器将直流电压变成正弦电压。汽车、船舶等远离供电区域时经常用到这种逆变过程。

正弦交流电压也可由函数发生器来获得。通过调节控制面板上的开关或手柄，就可以输出不同峰值和频率的正弦电压

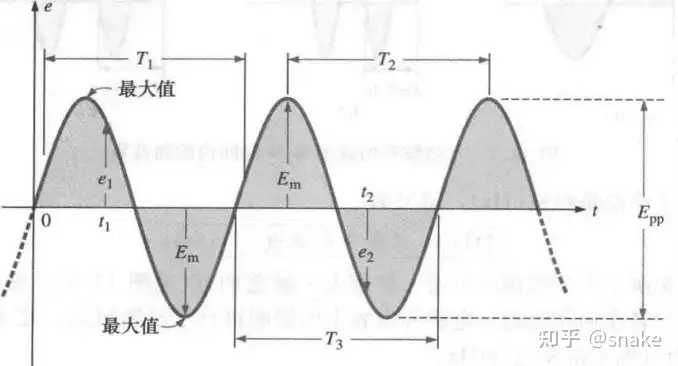
波形：变量的移动轨迹。这些变量可能是时间、位置、角度、弧度、温度等自变量的函数，这些函数的图像就是波形。

瞬时值：波形在任意时刻的大小，用小写字母表示。如图2所示的 e1e_{1} , e2e_{2} 。

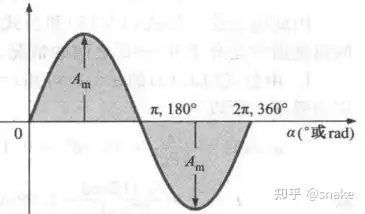
峰值振幅：如图2所示的波形，其平均值为0V；以平均值为起点量得的波形最大值，为峰值振幅，用大写字母表示，如图2中所示的电源电压 EmE_{m} 。

峰值：以零为起点量得的函数最大瞬时值，图2函数平均值为零，所以峰值振幅和峰值是一样的。

峰峰值：从波形的正向峰值到反向峰值的电压，即正向峰值与反向峰值之和，用 EppE_{pp} 或 VppV_{pp} 表示。

周期性波形：指波形在相同时间间隔下不断重复，图2所示为一个周期性波形。

周期（T）：波形循环变化一次所用的时间。

周波：一个周期时间内所包含的波形部分。如图3所示，T1，T2，T3所对应的周波不同，但它们都以一个周期为时间界限，因此都满足周波的定义。

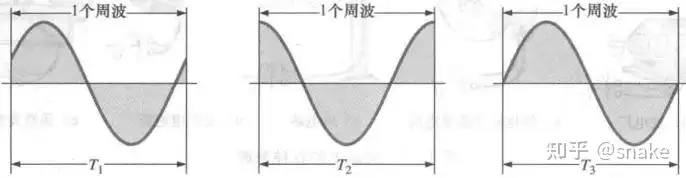
频率（f）：每秒出现的周波数，如图4所示，a)的频率是每秒钟一个周波，b)的频率是每秒钟2.5个周波，c)的频率是每秒钟2个周波。

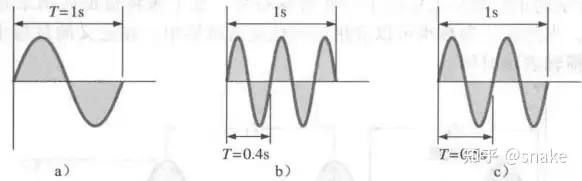
频率的测量单位是赫兹（Hz），定义为：

1Hz = 每秒1个周波（c/s）

单位赫兹来源于科学家海因里希·鲁道夫·赫兹的姓。赫兹对交流电压、交流电流以及二者作用在电阻、电感和电容上的影响进行了早期研究。北美的电网频率标准是60Hz，而欧洲大部分是50Hz。

像其他所有标准一样，任何一个与标准相左的改吧都会带来麻烦。1993年德国柏林允许接受所有输出频率在50.3-51Hz的交流电力，这一举动导致时钟每天快4分钟。结果报警器总是过早关闭，录像机也在节目结束之前提前关闭，时钟需要不断地重新校对。直到1994年，当电力输送至欧洲其他国家时，50Hz这一精确的频率标准又重新确立，事情才再次回到正轨。

2. 正弦波形

在所有交流波形中，只有正弦波通过电阻、电感和电容元件时，波形不会发生改变（或者说畸变）。

也就是说，如果电阻、电感或者电容上施加正弦电压（或流经正弦电流），那产生的电流（或电压）也是正弦量。但如果是其他信号的交流波形，比如方波或三角波施加在电容、电阻、电感上，将不会获得相同性质的输出。

如图5所示 。

对弧度作如下定义：一段弧长等于圆半径的弧，它所对应的圆心角称为1弧度。即

1rad=57.296°≈57.3°1rad = 57.296°\approx57.3°

一个完整圆周的弧度数是2π。

2πrad=360°2π rad = 360°

横轴的计量单位不仅可以是时间，还可以是角度或者弧度。如图6所示：

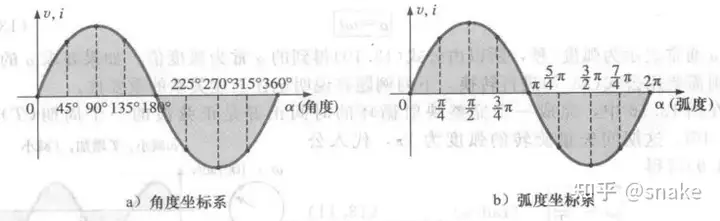
3. 角速度

一个有趣的现象是：一个以某点为中心做匀速圆周运动的矢量，其在垂直方向上的映射可以衍生出正弦波形。如图7所示。

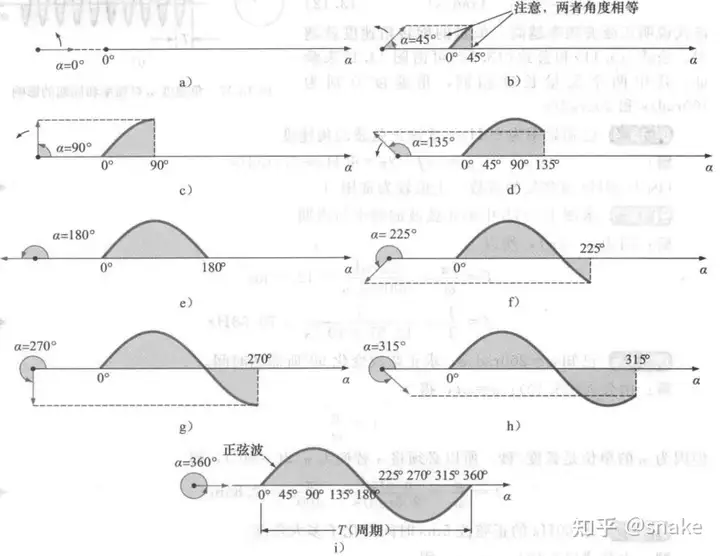
矢量围绕中心点旋转的速度称为角速度。角速度定义为：

角速度转角（角度或弧度）时间（秒）角速度=转角（角度或弧度）时间（秒）角速度 = \frac{转角（角度或弧度）}{时间（秒）}

角速度用小写希腊字母 ω\omega 表示，那么：

，ω=αt，α=ωt\omega = \frac{\alpha}{t}，\alpha = \omega t

很显然，完成一个完整映射循环的时间正好是正弦波的一个周期（T），这期间矢量旋转的弧度是2π，带入上式，可得：

（）ω=2πT（rad/s）\omega = \frac{2\pi}{T} （rad/s）

上式说明，正弦波形的周期越短，或者矢量旋转一周所需的时间越短，其旋转角速度就越大。

联系频率的定义，f=1/T，所以：

（）ω=2πf（rad/s）\omega = 2\pi f （rad/s）

这说明正弦波频率越高，角速度就越大。

3. 正弦波形的数学表示

正弦波的基本数学表达式为：

AmsinαA_{m}sin\alpha

式中， AmA_{m} 是波形的峰值或称幅值， α\alpha 为横轴的坐标。波形如图8所示。

等式 α=ωt\alpha = \omega t 说明，旋转矢量转过的角度α，由旋转角速度和矢量旋转时间所决定。例如，在一定角速度下，矢量的旋转路径越长（也即时间t越长），矢量旋转的角度数或者弧度数就越大。将这一情况与正弦波联系在一起，可知，在一定角速度下，时间越长，产生的周波个数越多；而在一定时间内，角速度越大，产生的周波数就越多。

可知，正弦波的一般形式可写为：

，为横轴坐标。Amsinωt，ωt为横轴坐标。A_{m}sin\omega t ，\omega t为横轴坐标。

对于电压和电流来说，一般形式为：

i=Imsinωt=Imsinαi = I_{m} sin\omega t = I_{m} sin\alpha

e=Emsinωt=Emsinαe = E_{m} sin\omega t = E_{m} sin\alpha

式中，带下标m的大写字母表示幅值，小写字母 ii 和 ee 分布表示电流和电压在任意时刻 tt 的瞬时值。

这种表示形式非常重要，它说明正弦交流电压或电流是一个与时间相关的函数，而示波器的横轴坐标恰好是时间。

4. 正弦波形的相位关系

同一坐标系中同一频率下，常用超前和滞后来说明两种正弦波形的相对关系。

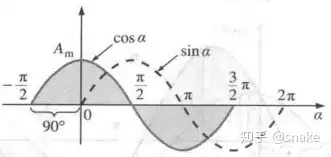
如图9所示，余弦波称为超前于正弦波90°，或者说正弦波滞后于余弦波90°，90°指的是两个波形之间的相角。

两波形之间的相角，可通过测量波形相同特征点（过零点、峰值点等）在横轴上的间距来获得。如果两波形特征点落在横轴同一点上，则称它们同相位。

正弦和余弦之间的几何关系如图10所示。

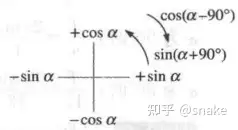
例如， 以+sinα+sin\alpha 为起始位置时，我们会发现沿着逆时针方向旋转了90°后，即： sin(α+90°)=cosαsin(\alpha+90°) = cos\alpha

还有：

）−sinα=cos(α+90°）=sin(α±180°)-sin\alpha = cos(\alpha+90°）= sin(\alpha±180°)

······

此外，需注意：

sin(−α)=−sinαsin(-\alpha) = -sin\alpha cos(−α)=cosαcos(-\alpha) = cos\alpha

如果正弦表达式写做：

e=−Emsinωte = -E_{m}sin\omega t

负号与正弦表达式联系在一起，这不是说峰值是负的。上式是下式的一种方便写法：

e=Em(−sinωt)e = E_{m}(-sin\omega t)

又因为： −sinωt=sin(ωt±180°)-sin\omega t = sin(\omega t ± 180°)

所以表达式也可以写做：

e=Emsin(ωt±180°)e = E_{m}sin(\omega t±180°)

说明负号可以用±180°的相位来替代，二者的波形能清楚的反映出它们之间的等价关系，函数存在两种正确的数学表达式。

【下一篇：正弦电路的元件和相量】