热电效应?

电热和热电明显是有关联的。用热力学语言来说，他们都是热流动力、粒子流动力耦合项的效应。

可以看一下这篇文章：不可逆过程热力学 – 知乎 (zhihu.com)

摘录一段文章中介绍热电效应的内容：

温差电效应

电路中同时存在温度梯度和化学势梯度时，将同时产生热流和粒子流（电流），从而产生以下五种效应：

泽贝克(Seebeck)效应；佩尔捷(Peltier)效应；汤姆逊(Thomson)效应；焦耳(Joule)热效应；热传导过程

注：由于我们现在考虑的都是均匀导体，所以可以认为除了和温度相关的化学势以外，只有电势；也即 −eE→=−∇μ-e\vec E=-\nabla\mu 。

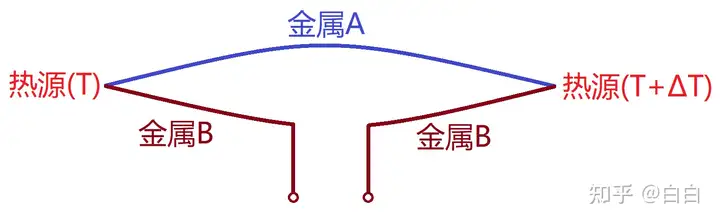
1、泽贝克效应

两个不同金属接成热电偶，在接头处保持不同温度。这样，A金属内有温度梯度；由于在不同温度下和A接触，B（左）和B（右）的化学势不同。于是，在两端口之间产生电动势：

dV=ϵABdT\mathbb dV=\epsilon_{AB}\mathbb dT\\

直接分析端口，可以知道 −edV=dμ-e\mathbb dV=\mathbb d\mu 。

对于金属A分析：A的热流动力被限制。 Xn=−LqnLnnXqX_n=-\frac{L_{qn}}{L_{nn}}X_q ； Xq=∇1TX_q=\nabla\frac1T ， Xn=−1T∇μX_n=-\frac1T\nabla\mu

从而 dμ=LqnLnndTT\mathbb d\mu=\frac{L_{qn}}{L_{nn}}\frac{\mathbb dT}T ； dV=−1eLqnLnndTT\mathbb dV=-\frac1e\frac{L_{qn}}{L_{nn}}\frac{\mathbb dT}T 。由于A与B的动理系数不同，会导致积累的 dV\mathbb dV 也不同，是即泽贝克效应。

在泽贝克效应的唯象理论中，我们通常写成 dV=(SA−SB)dT\mathbb dV=(S_A-S_B)\mathbb dT ， SS 为泽贝克系数。可以看出 SS 就是 −1eLqnLnn1T-\frac1e\frac{L_{qn}}{L_{nn}}\frac1T 。需要注意的是，泽贝克系数和动理系数通常是和温度相关的。

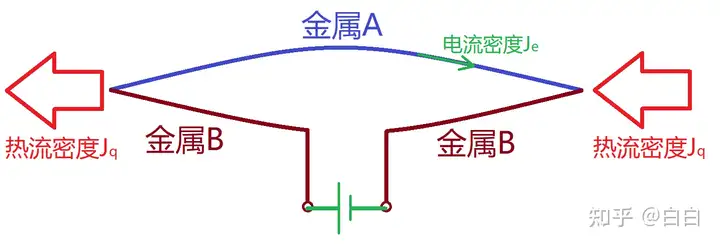
2、佩尔捷效应

两个不同金属相连接，保持两金属温度相同且不变，并通电流。这样，金属内有化学势梯度；由于耦合，也会产生热流。

Jq=πABJeJ_q=\pi_{AB}J_e\\

Je=−eJnJ_e=-eJ_n ；没有热流动力（控制了温度不变且均匀）。从而反解得粒子流动力 Xn=1LnnJnX_n=\frac1{L_{nn}}J_n ； Jq=LnqXn=−1eLnqLnnJeJ_q=L_{nq}X_n=-\frac1e\frac{L_{nq}}{L_{nn}}J_e 。对比得到 πAB=−1e(LnqLnn|A−LnqLnn|B)\pi_{AB}=-\frac1e\left(\frac{L_{nq}}{L_{nn}}\Bigg|_A-\frac{L_{nq}}{L_{nn}}\Bigg|_B\right) 。

3、汤姆逊效应

当电流通过具有温度梯度的均匀导体时，导体除了放出焦耳热，还要放出或吸收另外的热量，称之为汤姆逊热。汤姆逊热功率密度为 p=−τJ→e⋅∇Tp=-\tau\vec J_e\cdot\nabla T 。

产热的本质应该是一种熵产生，也即应有 p=ΘTp=\Theta T 。我们可以看到，焦耳热对应的是粒子流动力和粒子流的熵产生；而这里的汤姆逊热就应该对应热流动力和粒子流耦合项的熵产生。

然而此时的 μ\mu 还有和温度相关的项，这和电子化学势的具体形式有关。所以我们会在后面介绍开尔文关系的时候把 τ\tau 算出来。

4、焦耳热效应

我们熟知 p=σE2p=\sigma E^2 。

我们考虑的情形下温度均匀，没有热流动力；粒子流动力被限制为 eE→T\frac{e\vec E}T 。再结合 J→e=σE→\vec J_e=\sigma\vec E ，知道： σ=e2LnnT\sigma=\frac{e^2L_{nn}}T 。

5、热传导过程

傅立叶热传导定律 J→q=−κ∇T\vec J_q=-\kappa\nabla T 。此处热流动力被限制为常数；粒子流动力无限制。

J→1=(L11−L12L21L22)X→1\vec J_1=\left(L_{11}-\frac{L_{12}L_{21}}{L_{22}}\right)\vec X_1 ，直接带入 1→q1\rightarrow q ， 2→n2\rightarrow n ，从而 κ=1T2(L11−L12L21L22)\kappa=\frac1{T^2}\left(L_{11}-\frac{L_{12}L_{21}}{L_{22}}\right) 。

另一种唯象的理论（从微观角度入手）可以参考这篇文章：

白白：玻尔兹曼方程及其应用12 赞同 · 6 评论文章82 赞同 · 29 评论文章

★、开尔文关系

我们刚才求出了其中四个热电系数。我们可以它们用来解出动理系数：

Lqq=T3σϵ2+κT2Lnq=−T2σϵeLqn=−T2σϵeLnn=Tσe2\begin{align}&L_{qq}=T^3\sigma\epsilon^2+\kappa T^2&&L_{nq}=-\frac{T^2\sigma\epsilon}e\\&L_{qn}=-\frac{T^2\sigma\epsilon}e&&L_{nn}=\frac{T\sigma}{e^2}\end{align}

并且容易观察出， π=Tϵ\pi=T\epsilon （是即开尔文第二关系）。

写出各个流，并且把我们不希望看见的 ∇μ\nabla\mu 消去，可以得到：

J→q=−TϵeJ→n−κ∇T\vec J_q=-T\epsilon e\vec J_n-\kappa\nabla T ，并注意到 J→e=−eJ→n\vec J_e=-e\vec J_n ，可以写成 J→q=TϵJ→e−κ∇T\vec J_q=T\epsilon\vec J_e-\kappa\nabla T 。

顺便写出用温度和电流表示的化学势梯度： ∇μ=eσJ→e+eϵ∇T\nabla\mu=\frac e\sigma\vec J_e+e\epsilon\nabla T （后面会用到）。

考察一下熵流： J→s=J→qT=ϵJ→e−κT∇T\vec J_s=\frac{\vec J_q}T=\epsilon\vec J_e-\frac\kappa T\nabla T ，可以明显地看出后一项是热传导引起的熵流；而前一项就是电流携带的熵流。

我们再来看汤姆逊系数：

注意到能量的连续性定理： −∂u∂t=∇⋅(J→q+μJ→n)-\frac{\partial u}{\partial t}=\nabla\cdot(\vec J_q+\mu\vec J_n) ，在这里因为电流是衡常的， ∇\nabla 不对 J→n\vec J_n 作用：

−∂u∂t=∇⋅(J→q+μJ→n)=∇⋅J→q+J→n⋅∇μ-\frac{\partial u}{\partial t}=\nabla\cdot(\vec J_q+\mu\vec J_n)=\nabla\cdot\vec J_q+\vec J_n\cdot\nabla\mu

全部写成温度和电流的形式：

∂u∂t=−∇⋅(TϵJ→e−κ∇T)+J→ee⋅(eσJ→e+eϵ∇T)=−TJ→e⋅∇ϵ−∇⋅(−κ∇T)+1σJ→e2\begin{align}\frac{\partial u}{\partial t}&=-\nabla\cdot(T\epsilon\vec J_e-\kappa\nabla T)+\frac{\vec J_e}e\cdot(\frac e\sigma\vec J_e+e\epsilon\nabla T)\\&=-T\vec J_e\cdot\nabla\epsilon-\nabla\cdot(-\kappa\nabla T)+\frac1\sigma\vec J_e^2\end{align}

分析一下各个项的物理意义：第二项应该是由于热传导过程而在局部积累的热；第三项就是焦耳热。那么余下的第一项就是汤姆逊热了。

注意到 ∇ϵ=dϵdT∇T\nabla\epsilon=\frac{\mathbb d\epsilon}{\mathbb dT}\nabla T ，那么汤姆逊热 pτ=−τJ→e⋅∇T=−TJ→e⋅dϵdT∇Tp_\tau=-\tau\vec J_e\cdot\nabla T=-T\vec J_e\cdot\frac{\mathbb d\epsilon}{\mathbb dT}\nabla T ，对比可知 τ=TdϵdT\tau=T\frac{\mathbb d\epsilon}{\mathbb dT} 。

开尔文第一关系： τ=TdϵdT\tau=T\frac{\mathbb d\epsilon}{\mathbb dT} ，或者写成当年开尔文写的形式： dπdT=τ+ϵ\frac{\mathbb d\pi}{\mathbb dT}=\tau+\epsilon 。

里面的热力学原理比较复杂，还是建议看文章里的推导。

白白：不可逆过程热力学48 赞同 · 18 评论文章