球体 体积公式推导 – 微积分应用

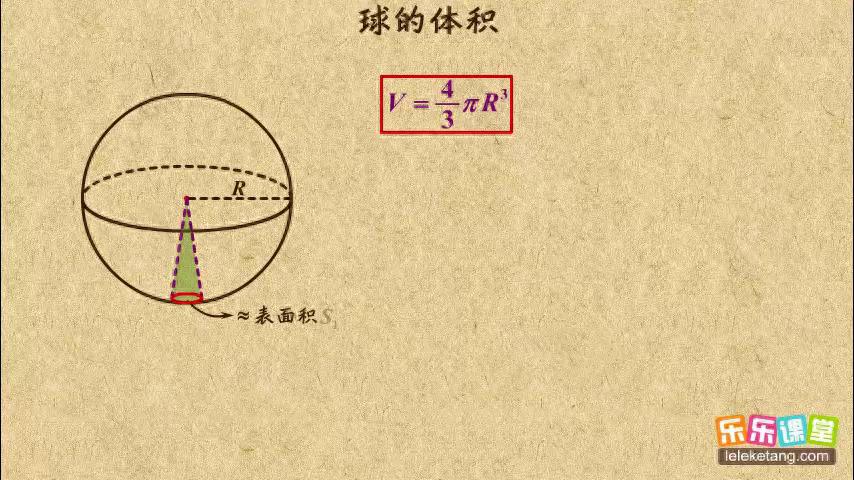
今天，我决定挑战自己，尝试推导球体的体积公式。作为一个刚开始学习微积分的学生，我对如何将积分应用到几何体中感到非常好奇。球体的体积公式 V=43πr3V=34​πr3 看起来既简洁又优美，但它是如何得来的呢？我决定一步步探索这个问题。

第一步：理解问题

首先，我需要明确什么是球体的体积公式。球体是一个三维几何体，所有点到中心点的距离都等于半径 rr。体积公式给出了这样一个几何体所占据的空间大小。

第二步：回顾相关知识

在开始推导之前，我回顾了一些相关的数学知识：

1. 圆的面积公式：A=πr2A=πr2。这是二维平面中圆的面积。
2. 积分的基本概念：积分可以用来计算曲线下的面积，或者通过旋转、叠加等方式计算三维物体的体积。
3. 旋转体的体积：通过旋转一个二维图形可以生成三维物体，其体积可以通过积分计算。

第三步：选择推导方法

我了解到，有多种方法可以推导球体的体积公式，包括：

1. 圆盘的积分方法：将球体看作由无数个薄圆盘叠加而成。
2. 壳方法：使用圆柱壳来积分。
3. 极坐标方法：在极坐标下进行积分。
4. 几何方法：如阿基米德的几何论证。

作为初学者，我决定选择圆盘的积分方法，因为它看起来最直观，也与我学过的积分知识最为接近。

第四步：建立坐标系和模型

为了使用圆盘的积分方法，我需要建立一个坐标系来表示球体。我选择将球体的中心放在三维直角坐标系的原点 (0,0,0)(0,0,0)。

球体的方程可以表示为：x2+y2+z2=r2x2+y2+z2=r2

为了计算体积，我可以考虑沿着 zz-轴将球体“切片”，即用平行于 xyxy-平面的平面去截球体，得到一系列的圆形截面。

第五步：表达单个圆盘的体积

考虑在高度 zz 处的一个薄片，其厚度为 dzdz。这个薄片可以近似为一个非常薄的圆柱体（即圆盘）。

从球体的方程 x2+y2+z2=r2x2+y2+z2=r2，在固定的 zz 处，x2+y2=r2−z2x2+y2=r2−z2。这表示在高度 zz 处的截面是一个半径为 r2−z2r2−z2​ 的圆。

因此，这个圆盘的面积为：A(z)=π(半径)2=π(r2−z2)A(z)=π(半径)2=π(r2−z2)

圆盘的体积为面积乘以厚度：dV=A(z) dz=π(r2−z2) dzdV=A(z)dz=π(r2−z2)dz

第六步：积分求总体积

为了得到整个球体的体积，需要将所有这样的薄圆盘的体积从 z=−rz=−r 到 z=rz=r 进行积分：V=∫−rrπ(r2−z2) dzV=∫−rr​π(r2−z2)dz

由于被积函数是关于 zz 的偶函数（即 (r2−z2)=(r2−(−z)2)(r2−z2)=(r2−(−z)2)），可以简化为从 0 到 rr 的积分，然后乘以 2：V=2π∫0r(r2−z2) dzV=2π∫0r​(r2−z2)dz

第七步：计算积分

现在计算这个定积分：∫(r2−z2) dz=r2z−z33+C∫(r2−z2)dz=r2z−3z3​+C

因此：2π[r2z−z33]0r=2π((r3−r33)−0)=2π(2r33)=43πr32π[r2z−3z3​]0r​=2π((r3−3r3​)−0)=2π(32r3​)=34​πr3

第八步：验证结果

为了确保我的推导没有错误，我进行了一些验证：

1. 量纲检查：体积的单位应该是长度的立方。r3r3 的单位是 length3length3，ππ 是无量纲的，所以 43πr334​πr3 的单位正确。
2. 特殊情况：当 r=1r=1，体积应该是 43π34​π，这与已知的单位球体积一致。
3. 与其他方法对比：查阅资料发现，其他方法如壳方法也能得到相同的结果，这增加了我的信心。

第九步：思考其他方法

为了更深入理解，我尝试思考另一种方法——壳方法。

壳方法简介

壳方法是通过将球体分解为一系列同心的圆柱壳来计算的。具体步骤如下：

1. 考虑球体的一个薄壳，半径为 xx，厚度为 dxdx。
2. 这个壳的高度可以通过球体的方程 x2+y2+z2=r2x2+y2+z2=r2 得到。在 xyxy-平面，高度 hh 对应于 zz 的范围，即 z=±r2−x2z=±r2−x2​，所以高度 h=2r2−x2h=2r2−x2​。
3. 圆柱壳的表面积为 2πxh=2πx⋅2r2−x2=4πxr2−x22πxh=2πx⋅2r2−x2​=4πxr2−x2​。
4. 壳的体积为表面积乘以厚度 dxdx：dV=4πxr2−x2 dxdV=4πxr2−x2​dx。
5. 积分从 x=0x=0 到 x=rx=r：V=∫0r4πxr2−x2 dxV=∫0r​4πxr2−x2​dx

计算壳方法的积分

令 u=r2−x2u=r2−x2，则 du=−2x dxdu=−2xdx，即 −du/2=x dx−du/2=xdx。

当 x=0x=0，u=r2u=r2；当 x=rx=r，u=0u=0。

因此：V=4π∫r20u(−du2)=4π⋅12∫0r2u1/2 du=2π[u3/23/2]0r2=2π⋅23r3=43πr3V=4π∫r20​u​(−2du​)=4π⋅21​∫0r2​u1/2du=2π[3/2u3/2​]0r2​=2π⋅32​r3=34​πr3

这与之前的结果一致，验证了壳方法的正确性。

第十步：总结与反思

通过两种不同的积分方法，我都得到了球体的体积公式 V=43πr3V=34​πr3。这让我对积分在几何中的应用有了更深的理解。圆盘方法更直观，适合初学者；而壳方法则提供了另一种视角，展示了数学的灵活性。

可能的误区与纠正

在最初的尝试中，我可能会犯以下错误：

1. 积分限的错误：最初可能会忽略从 −r−r 到 rr 的对称性，导致计算复杂化。通过利用对称性，可以简化计算。
2. 面积表达的错误：在表达圆盘面积时，可能会错误地认为半径是 rr 而不是 r2−z2r2−z2​，导致错误的积分。
3. 壳方法的高度表达：在壳方法中，可能会错误地认为高度是 r2−x2r2−x2​ 而忽略了上下两部分，实际上高度应为 2r2−x22r2−x2​。

通过仔细检查和验证，可以避免这些错误。

进一步的思考

除了积分方法，历史上阿基米德是如何推导球体体积的呢？阿基米德利用了一种巧妙的几何方法，将球体与圆柱和圆锥进行比较。他发现，一个球体的体积等于其外切圆柱体积的三分之二。具体来说：

• 外切圆柱的高度为 2r2r，半径为 rr，体积为 πr2⋅2r=2πr3πr2⋅2r=2πr3。
• 阿基米德证明球体的体积是圆柱的 2332​，即 23⋅2πr3=43πr332​⋅2πr3=34​πr3。

这种不依赖于微积分的方法展示了古代数学家的智慧。

数学公式的整理

为了更清晰地展示推导过程，我将主要步骤用数学公式整理如下：

圆盘方法：

1. 球体方程：x2+y2+z2=r2x2+y2+z2=r2。
2. 在高度 zz 处的截面半径：r2−z2r2−z2​。
3. 圆盘面积：A(z)=π(r2−z2)A(z)=π(r2−z2)。
4. 圆盘体积：dV=π(r2−z2) dzdV=π(r2−z2)dz。
5. 总体积：V=∫−rrπ(r2−z2) dz=2π∫0r(r2−z2) dz=2π[r2z−z33]0r=43πr3V=∫−rr​π(r2−z2)dz=2π∫0r​(r2−z2)dz=2π[r2z−3z3​]0r​=34​πr3

壳方法：

1. 壳的半径 xx，厚度 dxdx，高度 h=2r2−x2h=2r2−x2​。
2. 壳的表面积：2πxh=4πxr2−x22πxh=4πxr2−x2​。
3. 壳的体积：dV=4πxr2−x2 dxdV=4πxr2−x2​dx。
4. 总体积：V=∫0r4πxr2−x2 dxV=∫0r​4πxr2−x2​dx令 u=r2−x2u=r2−x2，du=−2x dxdu=−2xdx：V=4π⋅−12∫r20u du=2π[23u3/2]0r2=43πr3V=4π⋅−21​∫r20​u​du=2π[32​u3/2]0r2​=34​πr3

结论

通过上述详细的推导和验证，我确信球体的体积公式 V=43πr3V=34​πr3 是正确的。这一过程不仅让我掌握了积分在几何中的应用，也让我体会到了数学的严谨和美妙。未来，我期待能够探索更多几何体的体积和表面积公式，进一步丰富我的数学知识。