#头条创作游园会#
棱柱、棱锥、棱台的表面积和体积
1.棱柱、棱锥、棱台的表面积
①棱柱、棱锥、棱台的展开图形
ⅰ.棱柱的侧面展开图由若干个平行四边形拼成;
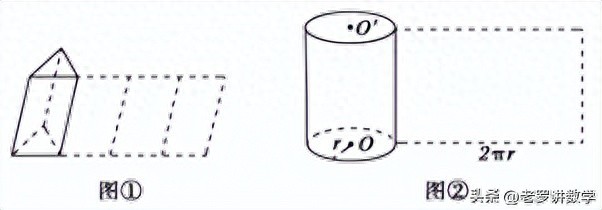
棱柱的侧面展开图与圆柱的区别
ⅱ.棱锥的侧面展开图由若干个三角形拼成;
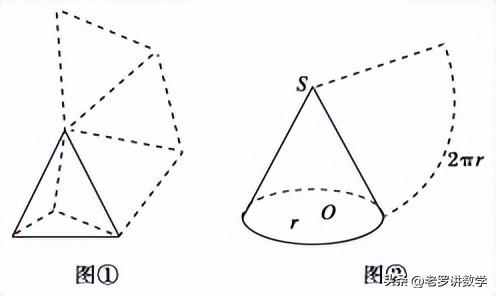
棱锥的侧面展开图与圆锥的区别
ⅲ.棱台的侧面展开图由若干个梯形拼成.

棱台的侧面展开图与圆台的区别
②棱柱、棱锥、棱台的表面积
ⅰ.棱柱的表面积:

ⅱ.棱锥的表面积:

ⅲ.棱台的表面积:


2.棱柱、棱锥、棱台的体积
①棱柱、棱锥、棱台的高
ⅰ.棱柱的高是指两底面之间的距离,即从一底面上任意一点向另一个底面作垂线,这点与垂足(垂线与底面的交点)之间的距离.
ⅱ.棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.
ⅲ.棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.

②棱柱、棱锥、棱台的体积


圆柱、圆锥、圆台、球的表面积和体积
1.圆柱、圆锥、圆台的表面积

圆柱、圆锥、圆台的表面积
2.圆柱、圆锥、圆台的体积

圆柱、圆锥、圆台的体积
3.球的表面积和体积
①球的表面积
若球的半径为

②球的体积
若球的半径为

③球的截面问题
ⅰ.用一个球面去截球,截面一定是圆面.
ⅱ.如果平面过球心,得到的截面圆为球的大圆(如地球仪上的经线圈与赤道所在的纬线圈);如果平面不过球心,得到的截面圆为球的小圆(如30°纬线圈).
ⅲ.如图,设小圆的圆心为





球的截面问题
④球与几何体外接、内切问题
ⅰ.解决与球有关的外接、内切问题的关键
⑴确定球心位置.
⑵构造直角三角形,确定球的半径.
即球心定位置,半径定大小.
ⅱ.球与多面体
⑴多面体的外接球:多面体的顶点均在球面上;球心到各个顶点距离相等(球半径).
⑵多面体的内切球:多面体的各面均与球面相切;球心到各面距离相等(球半径).
ⅲ.球与旋转体
⑴旋转体的外接球:旋转体的顶点在球面上;底面为球截面;球心在旋转轴上.
⑵旋转体的内切球:旋转体的各面均与球面相切;球心在旋转轴上.

为什么空间几何体对女生而言很难
空间几何体是初等几何教育的内容之一,是在初中平面几何学习的基础上,以空间图形的性质、计算,以及它们的应用为研究对象,研究三维空间中物体的形状、大小和位置关系的一门学科。空间几何体对部分学生而言可能具有挑战性,但这与性别并无直接关联。然而,确实存在一些观点认为,相对于男生,女生在学习空间几何体时可能会面临更多的困难。

1、空间想象能力的差异
部分女生可能在幼时较少接触和拆解构建立体物品,导致在大脑发展的关键期缺乏立体物象的感性积累,进而影响了空间想象能力的发展。
这使得她们在头脑中难以想象出立体的物象,从而在学习立体几何时感到困难。

2、教学方式的影响
传统的教学方式可能更注重理论知识的灌输,而缺乏对学生空间想象能力的培养和锻炼。
女生在数学学习过程中可能更注重细节和运算,而在空间想象和逻辑推理方面相对较弱,这可能与教学方式和个人学习习惯有关。
3、学习方法和策略的差异
女生在解决空间几何问题时,可能更倾向于使用记忆和复述的方法,而较少采用图形化或空间化的思考方式。
这可能导致她们在理解和解决复杂空间几何问题时遇到困难。
然而,需要强调的是,以上分析并不意味着女生在学习空间几何体方面必然存在劣势。实际上,许多女生在空间几何体方面表现出色,并且能够通过适当的训练和指导来克服这些所谓的“困难”。

女生提高空间几何体的学习能力的方法
1、增加实践经验
通过拆解、构建立体物品或参与相关的实践活动,增加对立体物象的感性积累。
使用手工泥、折纸等材料还原立体几何图形,将抽象的立体图形实体化。

2、培养空间想象能力
多进行画图训练,亲手画出立体图形,并反复练习以提高熟练度和准确性。
在头脑中固化已掌握的立体几何图形,通过反复“过电影”的方式加强空间再现能力。
3、采用多元化的教学方法
教师应采用多元化的教学手段,如微课、几何画板等辅助教学工具,帮助学生更好地理解空间几何体的概念和性质。
通过讨论、合作等方式激发学生的学习兴趣和积极性,培养他们的空间想象能力和逻辑推理能力。

4、调整学习方法和策略
鼓励女生采用图形化或空间化的思考方式来解决空间几何问题。
培养她们的问题解决能力和批判性思维,使她们能够更好地理解和应用空间几何体的知识。
综上所述,空间几何体对女生的难度并非由性别本身决定,而是受到多种因素的影响。通过适当的训练和指导,女生同样可以掌握空间几何体的知识和技能。
以下是相关练习题目(有需要的请收藏)






















免责声明:文章内容来自互联网,本站仅作为分享,不对其真实性负责,如有侵权等情况,请与本站联系删除。
转载请注明出处:高中数学: 简单几何体的表面积和体积讲解 https://www.zentong.com/edu/19681.html