直观系列（一）：球体积公式的动画推导 直观动画帮你

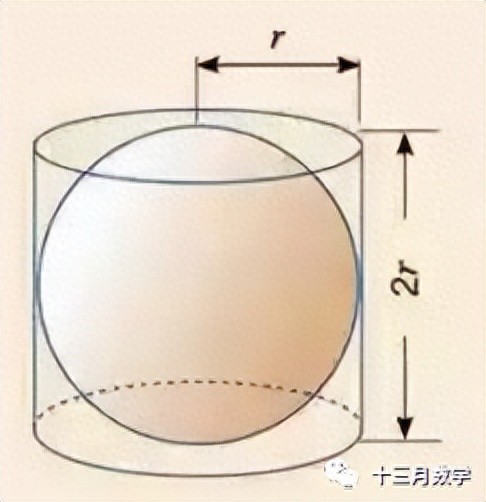
球的体积为什么是？

众所周知，球的体积等于三分之二πr的立方，这个公式通常是通过微积分的方法推导的。但是今天将用初等方法来证明这个问题。

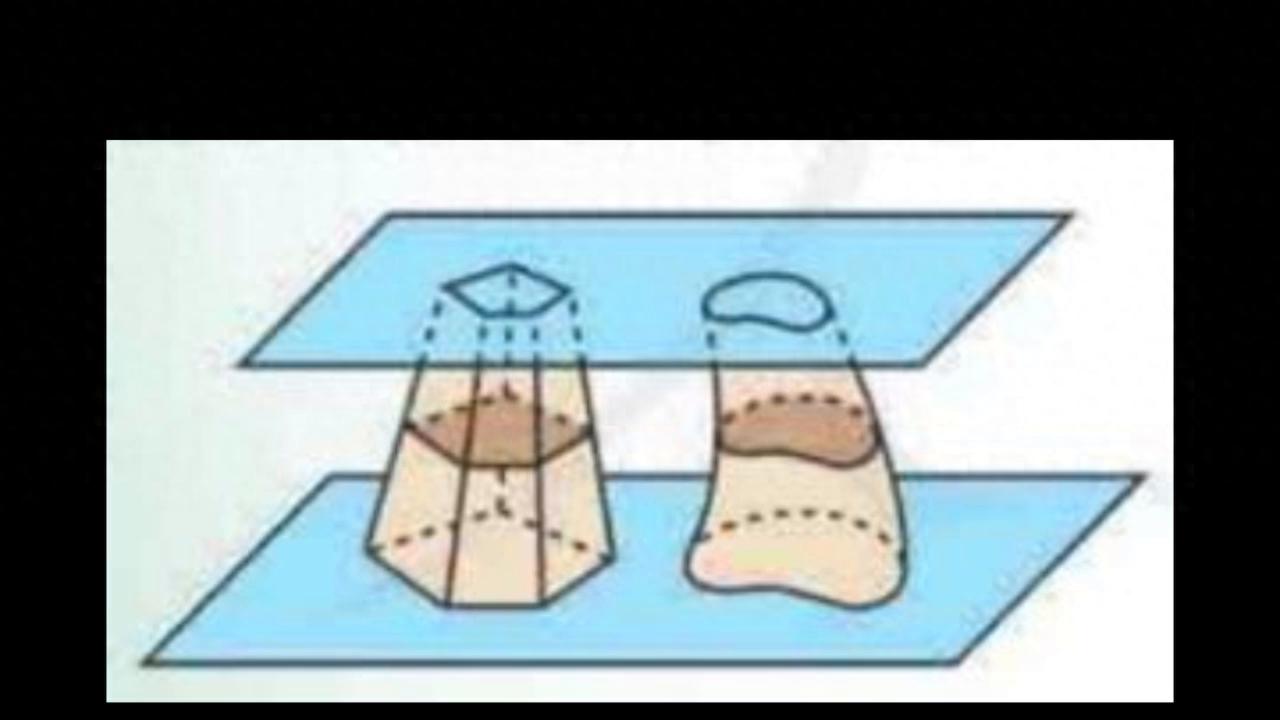
首先先看一个例子，两个平行平面之间加了两个形状不同的物体，两个平面之间有一个平行平面，分别和这两个物体结出了两个不同的形状。分别做如下标记：

·如果随着中间平面的上下移动，得到的截面面积始终相等，就能推出这两个物体的体积必定相等，这就是祖暅原理。

·如果S1=S2恒成立，则V1=V2，这个原理的发现者祖暅是祖冲织的儿子。

接下来将尝试使用这个原理。由于球的体积公式死时对我们是未知的，需要想办法将其转化为已知几何体的体积，与球关联度最高的就是圆柱以及圆锥，它们的体积公式是已知的。

接下来如果能构建出球和圆柱圆锥的体积关系，自然就能得到球的体积公式了。好在阿基米德已经帮我们找到了这个关系。如图所示，有球的体积等于圆柱体积减圆锥体积。

下面将结合动画予以证明。这里有一个球假设其半径为2，再做出一个底面原半径为2，高度为22的圆柱，以及顶点相对的底面原半径为2，高度分别也为2的两个圆锥，将它们放在同一水平面上。

接下来用水平面来截这三个几何体，就像动画里演示的一样，分别得到了三个蓝色的截面。将视角旋转到它们的上方，将看到三个圆。因为想证明球的体积等于圆柱体积减去两个圆锥体积，根据祖暅原理就需要证明第一个圆的面积等于第二个圆和第三个圆的面积差。

具体证明如下：假设截面在球心上方h的位置，在球体中取其球心、截面圆、圆心以及结线上任意一点连接得到直角三角形。根据勾股定理容易得到截面圆的面积等于πr乘以2方减h方。对于圆柱截面积显然横等于πr方。对于圆锥取其顶点截面圆、圆心和截面上任意一点连接得到一个直角三角形。

因为圆锥的高和半径都是2，所以由三角形相似可以证明这个三角形是等腰直角三角形，所以截面圆的面积为πh方。由此得到了三个面积公式，可以发现S1=S2-S3。所以根据祖暅原理有球的体积等于圆柱减去两个圆锥的体积，化简级得到球的体积公式。