牟合方盖

下面就是两个圆柱相交部分牟合方盖

牟合方盖是一种几何体，是两个等半径圆柱躺在平面上垂直相交的公共部分，r为圆柱半径。在古代牟是相同的意思，盖是雨伞的意思，所以“牟合方盖”指的就是把两个方形雨伞合在一起。

因为像是两个方形的盖子合在一起，所以被称作“牟合方盖”，可以利用牟合方盖推导计算出球体的体积。

这个牟合方盖要从著名数学家刘徽讲起，他在给《九章算术》写注时发现一个错误，书里认为即然在正方形里面内切一个圆，它的面积之比是π ：4

在圆柱体中内切一个球，它们的体积之比也是π ：4，

可事实当真如此吗？刘徽用“截面法”反驳了这一推论，即用刀片把圆柱从竖直方向一层层切开，你会发现除了最中间那层是正方形嵌着一个圆，其它都是一个长方形里嵌着一个小圆，它们的面积之比要小于π ：4，所以叠加起来，球体与圆柱的体积之比也是小于π ：4，

具体情况看下图

但仅仅证明了错误还不够，刘徽又开始研究，能不能找到一个比值恰好等于π ：4的几何体呢？

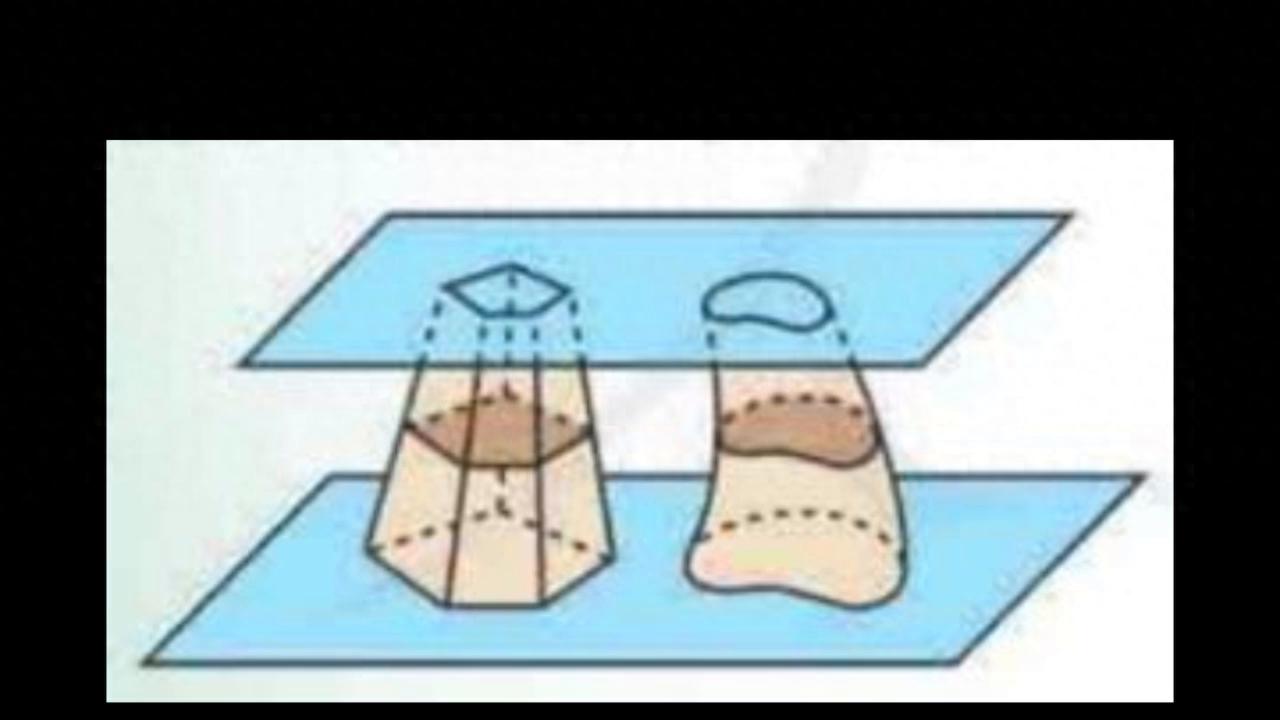
先画一个两个圆柱相交立方体，然后分别从前后和左右两个方向内切圆柱，它们相交的部分便是开提到的“牟合方盖”

下面我们可以再用“截面法”来切割一下

这时我们会发现，不论是从上到下，还是从左到右，每一个截面中圆与正方形的比值都是π ：4，所以它们的体积之比也是π ：4

这样我们只要求得牟合方盖的体积，就可以求得球体的体积了，但很可惜，刘徽最终也没能解决这个问题。直到两百多年后，祖冲之的儿子祖暅成功的解决了这个问题，我们先提到一个著名的数学定理。

祖暅原理：幂势既同，则积不空异。其中“幂”指的是截面积，势指的是立体的高，也就是说，如果两个几何体，在每一个相同高度处的截面积都相同，它们的体积也相同。看下图：四棱椎和圆椎截面积

祖暅利用这一原理计算出球的体积：

首先取边长为r的立方体与内切牟切方盖的八分之一。看下图：

在高h处将其截开、看下图：

看到这里，我们看后中国古人的智慧远远超过包括西方国家的整个世界。

我们还可以利用牟合方盖原理，用对比法推导出球的表面积公式：