球与几何体的外接、内切问题是立体几何的一个难点，也是近年高考的一个热点，今天我们专题讲解一下外接和内切球问题的解决方法。

解决与球的外接、内切问题的关键：

1. 确定球心位置

2. 半径：构造直角三角形，确定球的半径。

多面体的外接球问题：（常见几何体的外接球模型）

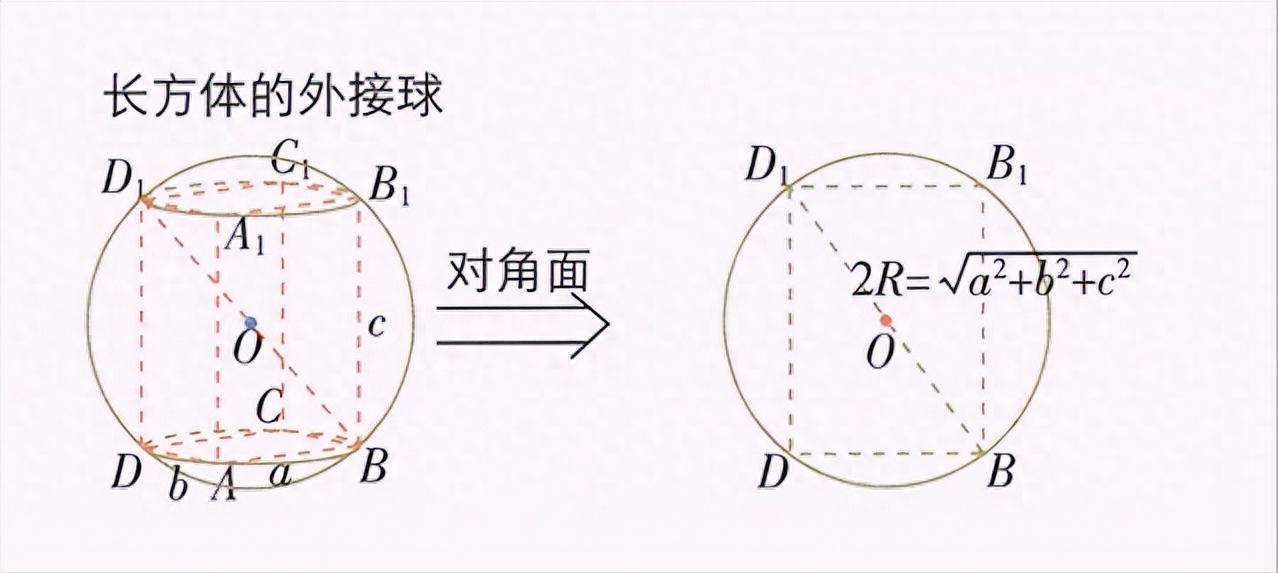
球心位置：长方体体对角线的中点，半径计算公式（R为外接球半径，a，b，c分别为长方体的长、宽、高）。

球心位置：正方体体对角线的中点，半径计算公式（R为外接球半径，a为正方体的棱长）。

球心位置：位于正棱锥（圆锥）的顶点与底面三角形外心连线（或延长线）上。

半径计算公式：在R t三角形中，（R为正棱锥的外接球半径，r为底面三角形ABC的外接圆半径，h为正棱锥的高。求解r可借助正弦定理

球心位置：位于过底面的外接圆圆心且垂直于底面的直线与垂直于底面的侧棱中垂面的交点。

半径计算公式：在R t三角形中，（R为的外接球半径，r为底面三角形ABC的外接圆半径，h为棱锥的高。

球心位置：上下底面外接圆圆心连线的中点。

半径计算公式：在R t三角形中，（R为的外接球半径，r为底面三角形ABC的外接圆半径，h为直棱柱（圆柱）的高。

多面体的内切球问题

内切球问题一般有两种方法：

1.利用内切球的定义，即球心到各面距离相等，找球心和半径，一般先做出多面体的对角线所在的截面，再利用定义求解。

2.利用等体积法求半径，球心到各个面的距离相等，可求出每个面的面积，再利用各个棱锥的体积之和等于多面体的体积球的内切球的半径。

我们通过下面例题来看一下等体积法的应用：

【例】已知正三棱锥的高为2，底面边长为2，求该三棱锥的内切球的表面积。

解：在正三棱锥中，过侧棱AB和球心作截面：

所以，BE是三角形BCD的高，是等边三角形BCD的中心，且AE为斜高，

因为BC=2，所以E=，又A=2，所以AE=

过O作OFAE于F，设内切球半径为r，则OA=2-r，因为，

所以可得，解得，r=

所有