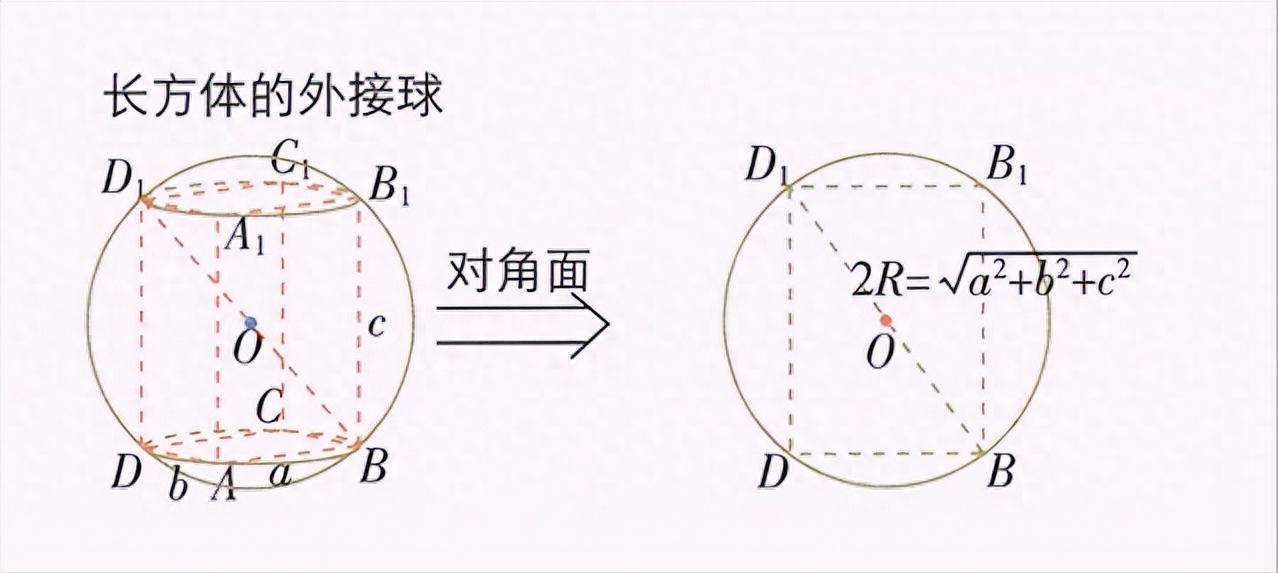
我们知道,球体表面积:

下面,我们用2种相对比较容易理解的方法来推导球体的表面积公式。
第1种方法:切片法+积分 推导球体表面积公式
1)将球心置于坐标系的原点O;
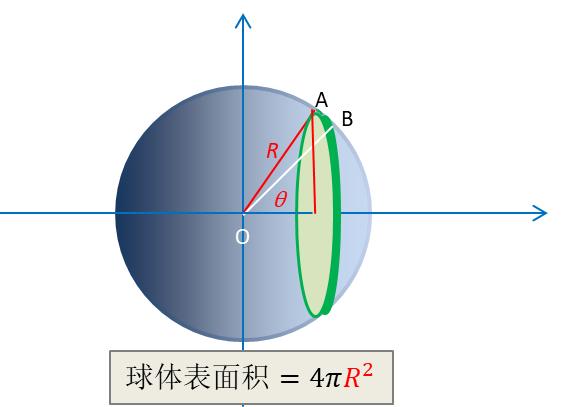
2)将球体无限切割成均匀薄片。
任取其中一张薄片分析

任意一张 厚度为dr的薄片
A,B分别为薄片的内侧点和外侧点
θ为A到圆心O的夹角

圆环内圆的半径:

圆环内圆的周长:

展开后的圆环近似为一个长方形,如图:

圆环展开后的图形,底为AB弧长,高为圆环内圆周长


球体表面面积S = 所有圆环面积之和

球体表面积=所有圆环面积之和
等价于以下积分形式:



延伸思考:
作球体切片积分时,设 圆环薄片圆心C到O的距离为r,薄片的厚度为dr,



注意用红色字体标注的部分,与已推导出来的积分式不一样

已推导出来的积分式
导致积分结果不一样,思考一下,为什么?
望感兴趣的朋友留言解答。
第2种方法:从球体体积公式推导球体表面积公式
将球体看作 由n个高度为dr的薄层构成
每剥开一层,球体的体积就减少dv,


对球体体积函数v(r)求导,可得到球体表面积关于半径的函数s(r):

免责声明:文章内容来自互联网,本站仅作为分享,不对其真实性负责,如有侵权等情况,请与本站联系删除。
转载请注明出处:球体表面积公式推导(2种方法) – 微积分应用 https://www.zentong.com/edu/19673.html