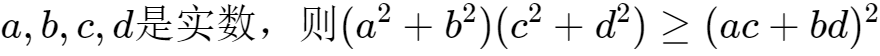高考数学 精华版 A02不等式 001 柯西不等式

高考数学 精华版 A02不等式 001 柯西不等式

————————–

〖小读物·多元代数式最值·方法总结〗

【1】两大类型

（1）有“条件等式”型；

条件等式的标准型是“多元代数式＝常数”。

（2）没有“条件等式”型，

此时结论式为多元分式和形式。

这类题多是“设计型”，所以都可以“特殊巧妙的方法”求解。

【2】指导逻辑：化归同类元项，没有例外的不二法门

个中含义，研读后续诸例体会。在此扼要解释。

以t(X)＝1表示条件等式；S(X)为结论式；形式上终是达成S(X)≥λ，或者S(X)≤λ；λ即为所求最值常数。

同类元项，有点内层函数相同的复合函数的意思。举例如，f(a＋b)与g(a＋b)是同类元项，f(a＋b)与f(ab) 则不是。

解答的方向，就是化t(X)与S(X)均表达为同类元项代数式，最终形式如S(X)≥S(t)或S(X)≤S(t)，S(t)是条件式为同类元的代数式；或S(X)表示成互为倒数的同类元项和，如 u＋1/u。

【3】两大方法·恒等变换（或恒等化简）

（1）换元化简：换元的实质是化简；

（2）因式分解·换元：因式分解显化“组份要素”，如质因数分解那样。常作为换元的前置技术，为换元及后续指明方向。

（3）分离变量·降元

（4）分式裂解（分离常数·结合待定系数法）

分式裂解总是以分母为单元。为简化过程，常常将非单项式的分母换元为单项式。

（5）常数替换

即以S(X)去乘t(X)＝1，得S(X)＝S(X) t(X)；也可局部替换（常作为齐次化手段）。

（6）拆配项（配凑法结合待定系数）

（7）其它：含参判别式法、齐次降元法、数形结合、三角代换、函数极值法等。

一个宗旨：化归同类元项

四个原则：能化简（含换元）则先/能因式分解则先/能分离变量降元则先/能分式裂解则先。

【4】两大方法·缩放变换（或缩放化简）

缩放变换，各不等式公式是缩放变换主要承载者。 （1）基本不等式；（2）均值不等式；（3）柯西不等式；（4）缩放通分 （典型但不限于权方和不等式）；（5）加减项；

最大值问题的缩放：整体/分子（≤），分母（≥）；

最小值问题的缩放：整体/分子（≥），分母（≤）；

无条件等式型·缩放变换

由于各变元的取值相互独立，可以放心使用各不等式公式进行缩放变换，包括局部缩放。

(1) 均值不等式

若与常数配合，还有降幂之效；

常用于局部缩放，过程中或有多次取等条件，但由于各变元独立，可同时满足；但取等条件次数，一般不宜超过元数。若超过须检验取等条件是否同时成立。

(2) 柯西不等式

一般是整体缩放，也就是只有单一的取等条件；

(3) 权方和不等式

一般是整体缩放，同样只有单一的取等条件；

有条件等式型·缩放变换

各变元取值不独立，利用不等式公式缩放时，必须满足：

(1) 均值不等式

如果有多次取等条件，唯有这些取等条件连同条件等式须同时满足时，方可使用。通常，要求这多个取等条件是相关联的。更多请研读后续诸例。

(2) 柯西不等式

一般是整体缩放，单一取等条件；可用。

(3) 权方和不等式

一般是整体缩放，单一取等条件；可用。