时序电路·专题01·基础知识-时序电路的作用是什么

一、时序电路的基本结构

时序电路的基本结构如图6.1.1所示，它由完成逻辑运算的组合电路和起记忆作用的存储电路两部分构成。

其中，存储电路由【触发器】或【锁存器】组成。

为了方便，图中各组逻辑变量均以向量形式表示，其中

输入信号：

、 I=(I1、I2,\dots,Ii)

I=(I_{1}、I_{2},…,I_{i}) ；输出信号：

、 O=(O1、O2,\dots,Oj)

O=(O_{1}、O_{2},…,O_{j}) ；激励信号：

、 E=(E1、E2,\dots,Ek)

E=(E_{1}、E_{2},…,E_{k}) ，可以驱动存储电路转换为下一状态；状态信号：

、 S=(S1、S2,\dots,Sm)

S=(S_{1}、S_{2},…,S_{m}) ，表示存储电路的状态，亦称为状态变量；它表示时序电路当前的状态，简称现态。

状态变量 $S$ S 被反馈到组合电路的输入端，与输入信号 $I$ I 一起决定时序电路的输出信号 $O$ O ，并产生对存储电路的激励信号 $E$ E ，从而确定电路的下一状态，即次态。

于是，上述4组变量间的逻辑关系可用下列三个向量函数形式的方程来表达∶

式（6.1.1）表达了激励信号与输入信号、状态变量的关系，称为时序电路的激励方程。

式（6.1.2）表达了存储电路从现态到次态的转换，故称为状态转换方程，简称转换方程。其中， $Sn$ S^{n} 和 $Sn+1$ S^{n+1} 分别表示存储电路的现态和次态。

而式（6.1.3）表达了时序电路的输出信号与输入信号、状态变量的关系，称为输出方程。

上述三个向量函数形式的方程分别对应于表达时序电路的三个基本方程组∶

激励方程组转换方程组输出方程组

如上所述，时序电路是状态依赖的，故又称为状态机（State Machine，SM）。本章将只限于讨论有限数量的存储单元构成的状态机，因而其状态数也是有限的，称为有限状态机（Finite State Machine,FSM)。

由上述基本结构和方程可见，时序电路具有以下主要特征：

①时序电路由【组合电路】和【存储电路】组成。②时序电路的状态与时间因素相关，即时序电路在任一时刻的状态变量不仅是输入信号的函数，而且还是电路以前状态的函数，并由当前输入变量和状态决定电路的下一状态。③时序电路的输出信号由【输入信号】和【电路状态】共同决定。

二、异步与同步时序电路

异步时序电路同步时序电路（1）概括电路中触发器的时钟输入端没有连接在统一的时钟脉冲上，或电路中没有时钟脉冲（如SR 锁存器构成的时序电路），即【电路中各存储单元的状态更新不是同时发生的】所有触发器的状态更新是在同一时刻，其输出状态变换的时间差异很小（2）分类1）【脉冲异步】时序电路（由触发器构成）

2）【电平异步】时序电路（由锁存器构成）【脉冲同步】时序电路（由触发器构成）（3）状态转换取决于以任意时间间隔变化的输入信号序列在同一时钟脉冲源的同一边沿作用下同步动作的

2-1：异步时序电路

若电路中触发器的时钟输入端没有连接在统一的时钟脉冲上，或电路中没有时钟脉冲（如SR锁存器构成的时序电路），从而电路中各存储单元的状态更新不是同时发生的。则这种电路称为异步时序电路。

根据电路是对脉冲边沿敏感还是对电平敏感，异步时序电路又分为脉冲异步时序电路（由触发器构成）和电平异步时序电路（由锁存器构成）两种。

异步时序电路的状态转换取决于以任意时间间隔变化的输入信号序列，若有多个信号输出，其存储电路的状态转换因存在时间差异而可能造成短时间输出状态的不稳定，而且这种不稳定的状态有时是不容易判定的，常常给电路设计和调试带来困难。

2-2：同步时序电路

与异步时序电路不同，同步时序电路中存储电路状态的转换是在同一时钟脉冲源的同一边沿作用下同步动作的，它也称作时钟同步状态机（Clocked Synchronous SM），其结构如图6.1.2 所示。

同步时序电路的存储电路一般用【触发器】实现，所有触发器的时钟输入端都应接在同一个时钟脉冲源 $CP$ CP 上，而且它们的时钟脉冲触发沿也都应一致。因此，所有触发器的状态更新是在同一时刻，其输出状态变换的时间差异很小。

在时钟脉冲两次作用的间隔期间，从触发器输入到状态输出的通路被切断，即使此时输入信号发生变化，也不会改变各触发器的输出状态，所以较少发生因状态转换不同步而引起的输出状态不稳定的现象。更重要的是，其电路的状态很容易用固定周期的时钟脉冲边沿清楚地分离为【序列步进】。

其中，每一个步进都可以通过输入信号和所有触发器的现态单独进行分析，从而有一套较系统、易掌握的分析和设计方法。电路行为也很容易用 $HDL$ HDL 来描述。

所以，目前结构较复杂、运行速度较高的时序电路广泛采用同步方式来实现。很多大规模可编程逻辑器件的应用电路和专用集成电路的设计，也都采用同步时序电路的结构。

三、米利型和穆尔型时序电路

3-1：米利（Mealy）型

米利（Mealy）型时序电路的结构如图6.1.3所示。

事实上是将图6.1.2中的组合电路拆解成激励组合电路和输出组合电路两部分。

米利型时序电路的输出信号 $O$ O是状态变量 $S$ S和输入信号 $I$ I二者的函数，即 $O=h(I,S)$ O=h(I,S)。

这种时序电路在时钟脉冲的两个触发沿之间，输出信号随时可能受到非时钟同步的输入信号作用而发生变化，从而影响电路输出的同步性。

3-2：穆尔型

穆尔（Moor）型时序电路是米利型时序电路的一种特例，它的输出信号 $O$ O 仅仅是状态变量 $S$ S 的函数，即 $O=h(S)$ O=h(S) 。其结构如图6.1.4 所示。

穆尔型时序电路的输出信号只取决于与时钟同步的各触发器的状态，在时钟脉冲触发沿的间隔期间，不受非同步的输入信号影响。

实际上，米利型时序电路中有时也有一个或多个输出可能是穆尔型的，即它们的输出只取决于触发器的状态。在现代高速时序电路设计中，一般尽量采用穆尔型时序电路结构，以利于后续高速电路的同步。

在米利型时序电路的输出端增加一级存储电路，构成【流水线输出】形式，是将其转化为穆尔型电路的最简单的方法，电路结构如图6.1.5所示。

需要注意的是，流水线存储电路将把输出信号延迟一个时钟周期。

虽然流水线输出电路增加了一些逻辑元件，但它的输出信号同步特性更好，具有更好的稳定性和抗干扰性能。

四、时序逻辑电路功能的表达

时序电路功能常见表达形式：

逻辑方程组【转换表】【状态表】【状态图】时序图HDL语言

从理论上讲，有了激励方程组、转换方程组和输出方程组，时序电路的功能就被唯一地确定了。

但是，对于许多时序电路而言，仅从这三组方程还不易判断其逻辑功能，在设计时序电路时，也往往很难根据给出的逻辑需求直接写出这三组方程。因此，还需要用能够直观反映电路状态变化序列全过程的转换表，状态表和状态图来帮助。

三组方程、转换表、状态表和状态图之间可以实现相互转换，根据其中任意一种表达方式，都可以画出时序图。

下面通过实例介绍时序电路逻辑功能的前五种表达方法。

考虑图6.1.6所示电路，它由组合电路与存储电路两大部分组成。

其中，存储电路由两个 $D$ D 触发器 $FF0$ FF_{0} 、 $FF1$ FF_{1} 构成，二者共用一个时钟信号 $CP$ CP ，从而构成一个同步时序电路。

组合电路又分为激励电路和输出电路两部分。

电路的输入信号为

A

A ；输出信号为

、 X、Y

X、Y ；对触发器的激励信号分别为

D0

D_{0} 和

D1

D_{1} ；

Q0

Q_{0} 、

Q1

Q_{1} 为电路的状态变量。

从图中可以看出，输出信号 $Y$ Y 是状态变量 $Q0$ Q_{0} 、 $Q1$ Q_{1}和输入信号 $A$ A 的函数，所以从总体上看，这是一个米利型时序电路，但是，输出信号 $X$ X 纯粹由状态变量 $Q0$ Q_{0} 、 $Q1$ Q_{1}决定，电路中又存在一个穆尔型输出 $X$ X 。

4-1：逻辑方程组

上述三组方程中，激励方程组和输出方程组表达了时序电路中全部组合电路的特性，而转换方程组则表达了存储电路从现态到次态的状态转换特性。

转换方程两边的状态变量，分别以上标 $n$ n 表示现态，以上标 $n+1$ n+1 表示次态，以区别这两种不同的状态。

根据上述的转换方程组与输出方程组可以列出真值表如表6.1.1所示。

真值表的输入变量为 $Q1n$ Q_{1}^{n} 、 $Q0n$ Q_{0}^{n} 和 $A$ A ，输出变量为 $Q1n+1$ Q_{1}^{n+1} 、 $Q0n+1$ Q_{0}^{n+1} 和 $、 X、Y$ X、Y 。

由于该真值表反映了触发器从现态到次态的转换，故称为【状态转换真值表】。

一般来说，有 $m$ m 位状态变量和 $i$ i 位输入信号，就存在 $2m+i$ 2^{m+i} 种状态-输入组合，真值表就应有 $2m+i$ 2^{m+i}行。

4-2：转换表

在分析和设计时序电路时，更常用的是【转换表】，如表6.1.2 所示。它与表6.1.1完全等效，但形式更紧凑明了。

表6.1.2用矩阵形式表达出在不同现态和输入条件下，电路的状态转换和输出逻辑值。

表中，输出信号 $X$ X 是穆尔型输出，故将其与现态 $Q1nQ0n$ Q_{1}^{n}Q_{0}^{n}对应的逻辑值单列一栏；

输出信号 $Y$ Y 的逻辑值不仅取决于 $Q1n$ Q_{1}^{n}和 $Q0n$ Q_{0}^{n}，而且会跟随 $A$ A 变化，所以表示在 $A=0$ A=0 和 $A=1$ A=1 两栏的斜线后面。需要注意的是，虽然它与斜线前的次态 $Q1n+1Q0n+1$ Q_{1}^{n+1}Q_{0}^{n+1}列在一起，但仍是现态 $Q1nQ0n$ Q_{1}^{n}Q_{0}^{n}和输入 $A$ A 的函数。

4-3：状态表

转换表以各触发器逻辑值的编码表示时序电路的状态。

在分析一个电路时，给每个编码状态分别赋予一个具体名称有时更便于与实际问题结合进行分析和记忆；时序电路设计过程中，在尚未进行状态分配之前，也必须首先给各个状态命名，以表达状态之间的转换关系。

在本例中，可以简单地命名4个状态为

00=a01=b10 =c11=d

当然，也可以用意义更明显的中、英文单词或数字来对状态命名。

将表6.1.2中 $Q1Q0$ Q_{1}Q_{0} 的状态用其状态名代替，则得到表6.1.3所示的状态表。

表中， $Sn$ S^{n} 表示现态， $Sn+1$ S^{n+1} 表示次态，斜线后的逻辑值为输出变量 $Y$ Y 的值。和转换表相比，使用状态表更容易理解时序电路的行为和结果。

如果状态命名合理，即使较复杂的时序电路，直接通过状态名就可以得到各状态的实际意义和转换关系。但是，状态表中的状态变量没有标明编码，与时序电路的3个逻辑方程组及实际电路图难以联系，这方面的信息少于转换表。转换表和状态表虽然形式和内容相似，然而在应用上是有差别的。

4-4：状态图

将表6.1.3的状态表转换为如图6.1.7（a）所示的状态图，可以更直观形象地表示出时序电路运行中的全部状态、各状态间相互转换的关系以及转换的条件和结果。

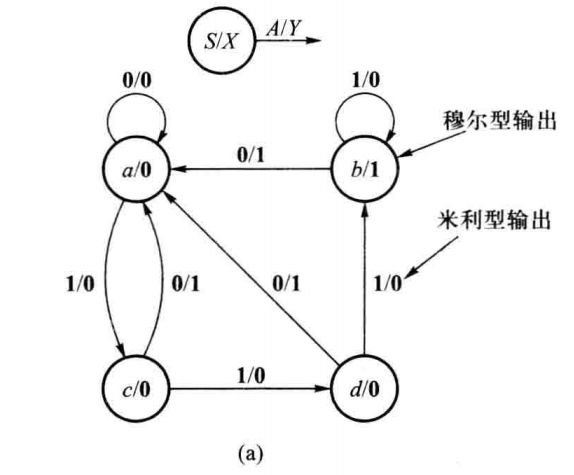
图中，每一个圆圈都对应着一个状态，圆圈中标出状态名；每一个带箭头的方向线都表示一个转换，箭头指示出状态转换的方向。当方向线的起点和终点都在同一个圆圈上时，则表示状态不变。引起该状态转换的输入变量逻辑值标在方向线旁斜线【左侧】，如图中 A 值。

米利型输出变量的逻辑值标在方向线旁斜线右侧，是本次状态转换前的逻辑值，如图中 Y 值，它由方向线起点的状态和斜线前的输入变量共同决定。而穆尔型输出变量的逻辑值则标在圆圈内的状态名后，因为状态一旦确定，其输出值随之确定，如图中 X 值。

当设计时序电路时，【首先】需要画出这种形式的状态图，以明确状态的数目、状态转换的方向以及状态转换的条件和相应的输出信号。

状态图也可以与转换表相对应，如图6.1.7（b）所示，圆圈中以二进制编码表示状态，在分析时序电路时可先得到这种形式的状态图，然后再进一步研究其功能。

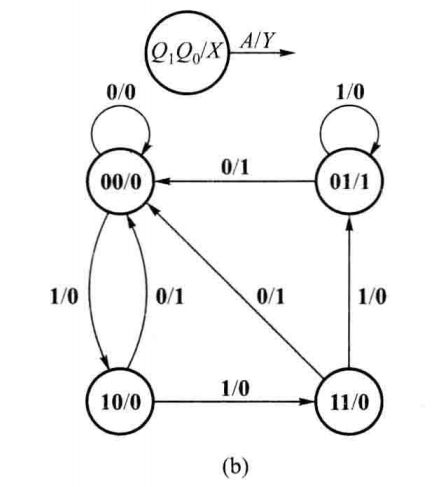
需要强调指出，图6.1.7（a）或（b）中状态转换的方向，取决于电路中下一个时钟脉冲触发沿到来前瞬间的输入信号。如果在此之前输入信号发生改变，则状态转换的方向也会立即改变。

例如图6.1.7（a）中，当处于状态 c 时，如果输入 A 保持为1，则输出 Y 为0，下一状态将转换为 d ; 若在下一个时钟脉冲触发沿到来之前， A 由1变化为0，则 Y 立即变化为1，下一状态将转换为 a 。

绘制状态图时需要注意不能漏画方向线。原则上，以某一状态为起点的方向线数量应为2^{i} 根， i 为电路输入变量的数目，即输入变量的每一种组合应当对应 1根方向线。例如，在图6.1.7 的状态图中只有一个输入变量 A ，共有 2^{1} 种组合∶ A=0 和 A=1 ，所以从每个状态都引出两根方向线。

当出现输入变量不同而方向线的起点和终点一致时，可以合并方向线。例如5.5.2 小节中讨论的 JK 触发器状态图，它有两个输入变量 J、K ，以每个状态为起点的方向线原应当有2^{2}=4 根，经合并后仅余两根，如图5.5.3所示，从而使状态图得到简化。

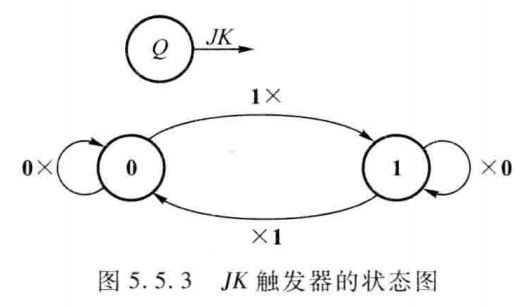
以图中触发器状态 Q=0 为例，转换到状态 Q=1 的方向线原有两根，输入变量的组合分别为 JK=10 和 JK=11 ，即同一方向上 K 是无关变量，于是可将两根方向线合并为一根，输入变量表示为 JK=1×。其余方向线的合并类推，最后得到简化的状态图。

因为人类对图形的理解能力远高于相应的表格、文字和公式，所以状态图在日益复杂的时序电路设计中愈显重要。从【状态图】出发，可以直接列出【状态表】，进而列出【转换表】。EDA 软件一般都可以以某种形式接受转换表的输入，有些软件甚至能以某种形式接受状态表或状态图的输入。

这样，在后续讨论的同步时序电路的设计中，从状态图以后的很多工作都可以由软件自动完成，【状态图】的描绘才是一项真正具有挑战性的工作。

4-5：时序图

与组合电路一样，波形图能直观地表达时序电路中各信号在时间上的对应关系。

通常把时序电路的状态、输出对输入信号（包括时钟信号）响应的波形图称为时序图。它不仅便于电路调试时检查逻辑功能、排查故障或差错，而且在运用 HDL设计电路时可用于电路的仿真从逻辑方程组、转换表或状态图都可以导出时序图。图6.1.6所示时序电路的时序图如图 6.1.8所示。

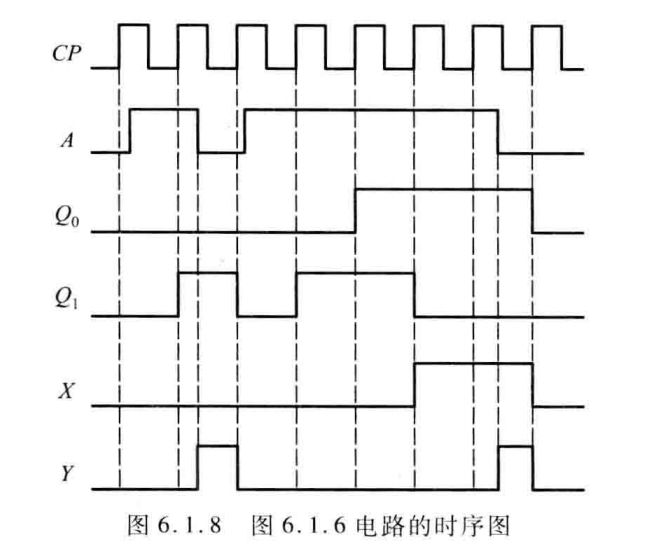
使用时序图时需要注意，有时它并不完全表达出电路状态转换的全部过程，而是根据需要仅画出部分典型的波形图，如图6.1.8中就没有表达出当状态Q_{1}Q_{0}为11而输入 A 为0时的状态转换波形和输出波形。

————

免责声明：文章内容来自互联网，本站仅作为分享，不对其真实性负责，如有侵权等情况，请与本站联系删除。
转载请注明出处：时序电路·专题01·基础知识-时序电路的作用是什么 https://www.zentong.com/zt/8245.html