为什么游戏本工作时CPU和GPU的温度可以达到那么高的温度？-游戏本打游戏的时候cpu温度

非专业人士，如有错误还请指正。

题目：为什么CPU和GPU可以达到那么高的温度？回答：因为在功耗和散热条件一定时芯片面积越小，温度越高。单独来看100W的发热量可能不算大，但是对于通常只有几百平方毫米的CPU和GPU，在空冷条件下会带来非常高的温度。而真空腔均热板/热管有着远高于普通金属和硅芯片的导热系数，使用均热板/热管连接散热鳍片等效于提高了CPU/GPU和散热鳍片的接触面积。

$P=a*C*V2*f$ P=a*C*V^2*f

在理想情况下，对于给定的CPU，其功率与电压的平方和频率成正比。而CPU消耗的绝大部分电能都转化成了热能，为了降低功耗和发热，降低工作电压和频率成了移动芯片的主流选择。[1][2][3]

$Pcpu=Pdyn+Psc+Pleak$ P_{cpu}=P_{dyn}+P_{sc}+P_{leak}

考虑CMOS反相器（非门）的能量转化，其功率可分为三部分：动态功率 $Pdyn$ P_{dyn} 、短路功率 $Psc$ P_{sc} 和漏电功率 $Pleak$ P_{leak} 。其中 $Psc$ P_{sc}和 $Pleak$ P_{leak}远小于 $Pdyn$ P_{dyn}，可以忽略。[1][2][3]

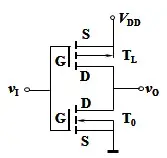
为什么游戏本工作时CPU和GPU的温度可以达到那么高的温度？-游戏本打游戏的时候cpu温度

CMOS反相器由一个P沟道MOS管（负载管）和一个N沟道MOS管（输入管）组成。负载管源极接高电压 $VDD$ V_{DD} ，输入管源极接地，负载管和输入管栅极接输入端，负载管和输入管漏极接输出端。要求 V_{GS(tr)N}＋|V_{GS(tr)P}|”> $＋ VDD>VGS(tr)N＋|VGS(tr)P|$ V_{DD}>V_{GS(tr)N}＋|V_{GS(tr)P}| ，其中 $VGS(tr)N$ V_{GS(tr)N} 为N沟道MOS管的开启电压， $VGS(tr)P$ V_{GS(tr)P} 为P沟道MOS管的开启电压。[4]

对于P沟道MOS管，栅极施加低电平导通，栅极施加高电平截止；对于N沟道MOS管，栅极施加高电平导通，栅极施加低电平截止。对于CMOS反相器，输入低电平时，负载管导通，输入管截止，输出高电平；输入高电平时，输入管导通，负载管截止，输出低电平。

把反向偏置的MOS管看成电容器，正向偏置的MOS管看成短路。由于任一工作状态下，CMOS反相器均有一个MOS管导通和一个MOS管截止，在变换状态时，截止的MOS管放电，导通的MOS管充电。由于电容中储存的能量为 $EC=12CV2$ E_{C}=\frac{1}{2}CV^{2} ，每个工作周期CMOS反相器变换两次工作状态，这些能量最终以焦耳热的形式释放，因此总共有 $Etr=CV2$ E_{tr}=CV^{2} 的电能被消耗。[3]

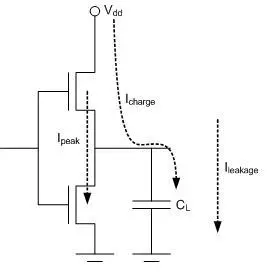
由一个周期内的能量消耗不难推出CPU的功率 $P\proptoC*V2*f$ P∝C*V^2*f ，考虑到CPU中包含成千上万个这样的门电路，因此有 $P=a*C*V2*f$ P=a*C*V^2*f 。[3]

如果把硅芯片看成在水平面上完全均匀的物体（近似处理，实际上并不可能。从单晶硅到硅芯片要进行蚀刻掺杂氧化金属化布线等处理，早已不再是硅单质），在发热功率恒定和相同的散热条件下，芯片面积越小，温度越高。

傅里叶定律：当物体内的温度只依赖一个空间坐标，而且温度分布不随时间发生变化时，热量沿温度降低的方向传导，称之为一维定态热传导，可用下式描述：

qx=-kdTdx

q_{x}=-k\frac{dT}{dx}

。

其中

qx

q_{x} 为热流密度，表征在与热传导方向x垂直的平面单位面积上，在x方向上传热的速率；T为温度，x为热传导方向坐标，k为物体的导热系数。此式表明热流密度

qx

q_{x} 与x方向上的温度梯度

dTdx

\frac{dT}{dx} 成正比，热流方向与温度梯度方向相反。[5]

想象这样一个场景：硅芯片上方紧贴着一块足够大的铜板，铜板上方有足够多的水，铜板下方除硅芯片外为理想真空。将硅和铜视为理想晶体，在水平方向上规则均匀排布。忽略硅芯片的厚度，铜板的厚度固定，水的温度恒定。忽略界面的空隙和气泡。忽略热对流和热辐射。忽略边界效应。

由已知条件容易得出铜板上表面的温度 $T2$ T_{2} 恒定。当硅芯片的发热功率 $P$ P 恒定时，体系最终会趋于稳态。此时所有热量均通过硅-铜界面竖直向上传导，符合一维定态热传导。

设铜板在竖直方向上的导热系数为 $k$ k ，铜板厚度为 $L$ L，硅芯片面积为 $A$ A 。根据傅里叶定律，可以计算出铜板下表面的温度 $T1$ T_{1} 。

对 $qx=-kdTdx$ q_{x}=-k\frac{dT}{dx} 进行积分，

$\int12qxdx=\int12-kdTdxdx$ \int_{1}^{2}q_{x}dx=\int_{1}^{2}-k\frac{dT}{dx}dx ，

解得 $qxL=k(T1-T2)$ q_{x}L=k(T_{1}-T_{2}) 。

$\int\intqxL=\int\intk(T1-T2)$ \int_{}^{}\int_{}^{}q_{x}L=\int_{}^{}\int_{}^{}k(T_{1}-T_{2}) ，

解得 $qxLA=k(T1-T2)A$ q_{x}LA=k(T_{1}-T_{2})A 。

由于 $P=qxA$ P=q_{x}A ，

因此 $T1=PLkA+T2$ T_{1}=\frac{PL}{kA}+T_{2} 。

这个结果是在理想化的条件下得出的。实际上硅芯片并非均匀的。芯片与散热装置之间存在空隙。桌面CPU采用钎焊/硅脂导热封装，散热器底座、热管和鳍片采用焊接方式连接，对热管进行压扁和折弯，对鳍片表面进行镀镍处理。这些因素都会在一定程度上降低散热效果。此外必须指出的是，这里忽略了水平方向上的热传导，在实际应用中由于硅芯片的面积有限，在硅芯片边缘与铜板之间的热传导是不均匀的。

参考

^abCPU power dissipation – Wikipedia https://en.wikipedia.org/wiki/CPU_power_dissipation^abWhy P scales as C_V^2_f is so obvious https://software.intel.com/content/www/us/en/develop/blogs/why-p-scales-as-cv2f-is-so-obvious.html^abcdWhy P scales as C_V^2_f is so obvious (pt 2) https://software.intel.com/content/www/us/en/develop/blogs/why-p-scales-as-cv2f-is-so-obvious-pt-2-2.html^CMOS反相器工作原理_主要特性_特点-维库电子通 http://wiki.dzsc.com/7202.html^热传导_百度百科 https://baike.baidu.com/item/%E7%83%AD%E4%BC%A0%E5%AF%BC

免责声明：文章内容来自互联网，本站仅作为分享，不对其真实性负责，如有侵权等情况，请与本站联系删除。
转载请注明出处：为什么游戏本工作时CPU和GPU的温度可以达到那么高的温度？-游戏本打游戏的时候cpu温度 https://www.zentong.com/zt/8182.html

为什么游戏本工作时CPU和GPU的温度可以达到那么高的温度？-游戏本打游戏的时候cpu温度

参考

相关推荐