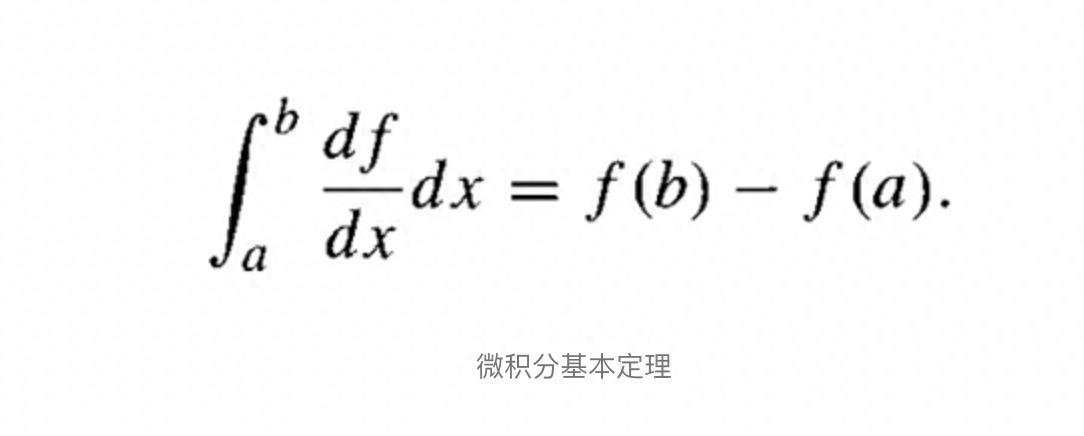代数学

什么是代数学？

代数学是一门数学分支，研究抽象数量和数量关系的结构和性质。它通过符号和符号操作来研究各种数学对象，如数字、变量、方程、多项式和函数，以及它们之间的操作和关系。代数学的研究范围包括代数方程、代数结构、线性代数、群论、环论、域论、模论和格论等。

代数学在数学中起着至关重要的作用。它不仅深入研究了数的性质和运算规律，还扩展到研究数学中的抽象结构和关系。代数学的方法和概念被广泛应用于各个领域，如物理学、计算机科学、经济学和工程学等。

代数学包括许多重要的概念和定理，如线性方程组、多项式和多项式方程、域和域扩展、群和群论、环和环论等。这些概念和定理对于解决各种实际问题和推动数学理论的发展都起着重要的作用。

总之，代数学是研究抽象数量和数量关系的分支学科，它不仅研究数的性质和运算规律，还研究数学中的抽象结构和关系，对于各个领域的数学和应用科学都具有重要意义。

代数学的基本概念，至少20条

以下是代数学的一些基本概念，总共有20条：

数字：代数中的基本单位，用来表示数量。变量：代数中表示未知数的符号，表达式中的字母通常用来表示变量。方程：数学等式，其中包含变量和恒定值，表达了两个数或表达式相等的关系。多项式：由多个项组成的代数表达式，每个项包含一个系数乘以一个变量的幂。系数：在多项式中与变量的乘积的常数部分。指数：在变量上方的小数字，表示变量的乘幂。线性方程组：一组方程，其中每个方程可以用一条直线表示。线性代数：研究线性方程组、向量和矩阵的数学分支。平方根：一个数的平方根是另一个数，使得它的平方等于给定的数。复数：由实部和虚部组成的数，包括实数和虚数。集合：一组元素的集合，可以是有限的，也可以是无限的。群：一个集合和一个二元运算，满足封闭性、结合律、恒等元素和逆元素的代数结构。环：一个集合和两个二元运算，满足加法的封闭性、结合律、交换律和加法单位元素。域：一个集合和两个二元运算，满足加法、减法、乘法和除法运算的规则。同态映射：两个代数结构之间的映射，保持运算结构的一致性。等价关系：一种二元关系，具有自反性、对称性和传递性。同余关系：整数之间的一种等价关系，两个整数在模意义下相等。不可约多项式：不能被分解为两个或更多的乘积的多项式。求和符号：用来表示对一系列数或表达式的求和。不等式：数学表达式中的关系符号，表示两个数或表达式之间的大小关系。

代数学的基本定理，至少20条

以下是代数学的一些基本定理，总共有20条：

一次方程定理：任何一次方程都有且仅有一个解。二次方程定理：任何二次方程都有两个解，除非判别式为零，此时有一个重解。四平方定理：任何正整数都可以表示为四个整数的平方和。复数根定理：任何非零多项式都有至少一个复数根。插值定理：通过已知点的坐标可以唯一确定一个插值多项式，从而通过其它点的插值值可以计算出未知点的函数值。唯一分解定理：任何自然数都可以唯一分解成质数的乘积。欧拉公式：在数学中，e^ix = cos(x) + isin(x)。贝祖定理：如果两个整数a和b不全为零，那么存在整数x和y，使得ax+by=gcd(a,b)，其中gcd(a,b)表示a和b的最大公约数。求根定理：任何方程组的解，可以通过求解伴随矩阵的特征值来获得。域的特征定理：如果域F中的特征不为零，则F中的特征是一个素数。根号2的无理性证明：根号2不是有理数。均值值定理：在一定条件下，函数在两个点之间的均值等于这两个点的斜率。逆矩阵定理：一个方阵有逆矩阵，当且仅当它是一个非奇异方阵（行列式不为零）。开尔文定理：代数曲线的分形维数出现在它的特征多项式的根中。分配律：在代数中，乘法对加法满足分配律。子空间定理：线性空间中的任何非空子集，如果对于该线性空间的加法和数乘封闭，那么它是该线性空间的子空间。群同构定理：如果有两个群G和H之间的同态映射，那么群的同态映射的像是G和H之间的同构。素数定理：在1到x之间的素数的个数近似等于 x / ln(x)，其中ln(x)是以自然对数为底的对数。牛顿-莱布尼茨定理：微积分中的基本定理，将一个函数的导数和定积分联系起来。卡诺图定理：布尔代数中，通过卡诺图可以将布尔表达式转化为逻辑门电路。

代数学的基本思想，至少20条

以下是代数学的一些基本思想，总共有20条：

抽象性：代数学研究抽象的数学结构，而不仅仅关注具体数值的计算。符号操作：代数学使用符号来表示数和运算，通过符号的操作来推导和研究数学关系。代数结构：代数学研究各种数学对象的结构和性质，如群、环、域等代数结构。同构：代数学强调通过同构的映射，研究不同的代数结构之间的相似性和等价性。研究关系：代数学关注数学对象之间的关系、运算和变换，以及这些关系的性质和规律。抽象代数：代数学发展了抽象代数的理论，研究代数结构的一般性质和共性规律。研究不变量：代数学通过研究不变量来揭示数学对象的特征和性质，并用于分类和比较不同的结构。推导和证明：代数学通过推导和证明来建立数学理论，揭示数学中的真理和规律。建立模型：代数学用代数结构来建立数学模型，用于解释和描述现实世界的问题和现象。解决方程：代数学研究如何解决方程，找到未知数的值，以及方程根和解的性质。多项式拟合：代数学使用多项式来逼近和拟合函数和数据，进行数值近似和插值。研究多元关系：代数学研究多个变量之间的关系，如多元方程组和多变量函数等。探索代数结构的运算：代数学研究代数结构中的运算，解析其性质和规律。探索代数对象的内在属性：代数学研究代数对象的内在属性，如多项式的次数、方程的判别式等。利用对称性：代数学利用对称性和群论的概念来研究对象之间的等价性和结构。利用代数工具解决实际问题：代数学利用代数工具和方法来解决实际问题，如物理、工程、经济等领域的问题。利用代数算法解题：代数学使用计算和算法来解决方程、求解根、计算多项式等数学问题。利用代数思想解决抽象问题：代数学通过抽象思维和逻辑推理，解决各种抽象问题和研究领域。发展新的代数理论和结构：代数学致力于发展新的代数理论、结构和方法，推动数学的发展和应用。推广和应用：代数学的思想和方法被广泛推广和应用于其他数学分支和各个领域的问题求解和理论研究。